タイトル
数学的な問題解決の基本となる数学化サイクル
関連する分野・授業 Categories or Related Class
算数Ⅰ、算数Ⅱ、算数科教育法Ⅰ、算数科教育法Ⅱ
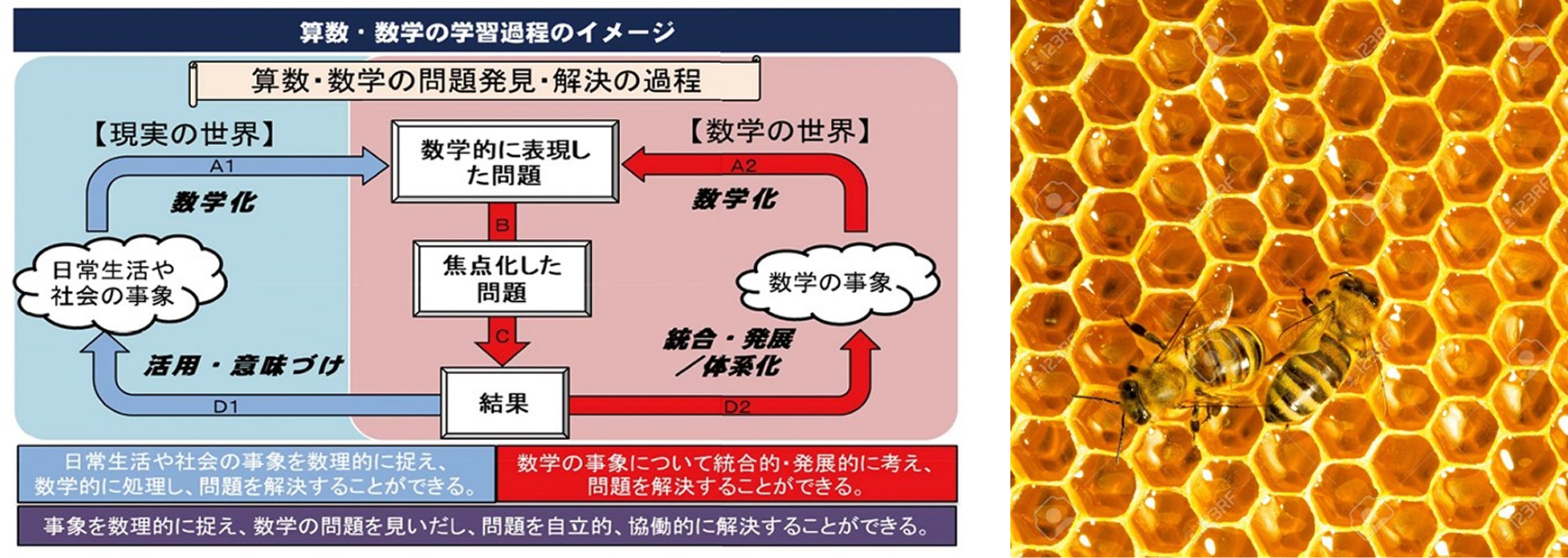
上の左図は『小学校学習指導要領(平成29年告示)解説算数編』(文部科学省、p.8)に示されている「算数・数学の学習過程のイメージ」です。これは、数学の原理・原則・性質・特性を用いて、現実的な問題を解く一連の流れを説明しています。
例えば、科目「算数Ⅰ」では「ハチの巣の部屋はなぜ正六角形なのか?」という問いを考えます。この問いを数学的に表現すれば、「正六角形は敷き詰め可能」となります。これを導入として、「敷き詰め可能な正多角形は何か?」という図形の敷き詰め問題を考えます。実際の操作で、正三角形、正四角形(正方形)、正六角形は敷き詰め可能であることは簡単に分かります。しかしながら、正四角形と正六角形は敷き詰め可能であるにもかかわらず、4と6の間にある正五角形では敷き詰めができません。なぜでしょうか。つまり、「敷き詰め可能な正多角形は何か?」という数学的な表現を含む現実的な疑問が生まれます。
「敷き詰め可能な正多角形は何か?」を解く過程で「方程式(n-2)(m-2)=4を解く(ただし、nとmは3以上の自然数)」という数学の問題が導かれます。このように、現実的な問題を数学の問題に変換することを「数学化」といいます。数学化を通じて、「敷き詰め可能な正多角形は何か?」という問題は、「方程式(n-2)(m-2)=4を解く」と数学の問題に翻訳されます。これを解くと、n=3,4,6が得られ、敷き詰め可能な正多角形は、数学的に、正三角形、正方形、正六角形の3つしかない、ことが得られます。なお、この3つの正多角形において、周の長さが等しい場合、最も一辺の長さが短くかつ面積が大きいものは正六角形になります。これを踏まえると、部屋の丈夫さと広さの観点から、ハチの巣の部屋が正六角形であることに納得できます。
とはいえ、「敷き詰め可能な正多角形は何か?」から「方程式(n-2)(m-2)=4」を導出することは必ずしも容易ではありません。「数学化」を算数の言葉で言えば「立式」です。「立式」は算数指導の要と言っても過言ではありません。算数で登場する立式に「敷き詰め問題の数学化」のような複雑なものはありません。そのため、算数指導において、数学化の重要性が見逃されがちであると言えるかもしれません。「立式」を数学化という重要な数学の一つとして捉え直し、より大きいなイメージを持って算数を指導できる教員を目指してほしいと思います。
プロフィール

- 教育学部
-
渡邊 耕二
Koji Watanabe
-
学位 分野・取得大学
博士(広島大学)
-
教授分野
算数科内容学、算数科指導法、教育の方法と技術、数学と生活、情報処理





